Math 1012 foundations of mathematics – Embarking on a journey through Math 1012: Foundations of Mathematics, we delve into the very essence of mathematical thought. This course provides a comprehensive exploration of the fundamental concepts that underpin the entire field of mathematics, laying a solid foundation for further mathematical endeavors.

From number systems and logic to algebraic structures, functions, and relations, we unravel the building blocks of mathematics, gaining a deep understanding of their properties and applications. Calculus, geometry, and mathematical proof are also integral parts of this foundational study, equipping us with the tools to tackle complex mathematical problems and unravel the mysteries of the world around us.

Introduction

Purpose and Scope of the Course

Math 1012 Foundations of Mathematics introduces the fundamental principles and concepts that underpin the entire field of mathematics. This course provides a rigorous exploration of the essential building blocks upon which all mathematical knowledge is constructed, laying the groundwork for a deep understanding of the subject.

Significance and Relevance of Foundational Concepts

Foundational mathematical concepts are not merely abstract ideas; they are the bedrock upon which all scientific and technological advancements rest. From the laws of physics to the development of computer algorithms, a solid grasp of mathematical foundations is indispensable. By delving into these concepts, students will gain a profound appreciation for the power and beauty of mathematics and its pervasive influence in shaping our world.

Number Systems and Logic

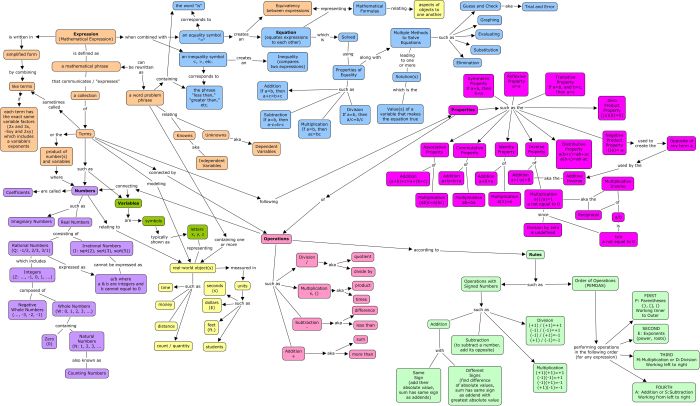
Number systems and logic form the foundation of mathematics. Number systems provide a way to represent and manipulate quantities, while logic provides the tools for reasoning and proving statements.

Number Systems

Number systems are sets of symbols used to represent quantities. The most common number systems are:

• Natural numbers: The set of positive integers 1, 2, 3, ….
• Integers: The set of natural numbers, their negatives, and zero …, -3, -2, -1, 0, 1, 2, 3, ….

• Rational numbers: The set of numbers that can be expressed as a fraction of two integers, a/b, where b ≠ 0.

• Real numbers: The set of all numbers that can be represented on a number line.

Logic

Logic is the study of reasoning and argumentation. It provides a set of rules for determining whether a statement is true or false based on its constituent parts.

The two main branches of logic are:

• Propositional logic: Deals with statements that are either true or false, such as “The sky is blue.”
• Predicate logic: Deals with statements that involve variables, such as “For all x, x + 1 > x.”

Set Theory

Set theory is a branch of mathematics that studies sets, which are collections of distinct objects. Set theory provides a foundation for many areas of mathematics, including number theory, algebra, and analysis.

Some of the basic concepts of set theory include:

• Sets: Collections of distinct objects.
• Elements: The objects that belong to a set.
• Union: The set of all elements that belong to either of two sets.
• Intersection: The set of all elements that belong to both of two sets.

Algebraic Structures

Algebraic structures are mathematical systems that consist of a set of elements and one or more operations on those elements. These operations satisfy certain axioms, or rules, that define the structure. Algebraic structures are used to study the properties of mathematical objects and to solve mathematical problems.Three

of the most important algebraic structures are groups, rings, and fields. A group is a set of elements with an operation that combines any two elements to form a third element. The operation must satisfy certain properties, such as associativity, identity, and inverse.

Rings and fields are similar to groups, but they also have additional operations that satisfy additional axioms.Algebraic structures are used in a wide variety of applications, including computer science, physics, and engineering. For example, groups are used to study symmetry in geometry, rings are used to study the structure of numbers, and fields are used to study the properties of polynomials.

Groups, Math 1012 foundations of mathematics

A group is a set of elements G with an operation

• that combines any two elements a and b to form an element c, written as a
• b = c. The operation

must satisfy the following axioms

* Associativity: For all a, b, and c in G, (a

• b)
• c = a
• (b
• c).

Identity

There exists an element e in G such that for all a in G, e

• a = a and a
• e = a.

Inverse

For each a in G, there exists an element b in G such that a

• b = e and b
• a = e.

Groups are used in a wide variety of applications, including computer science, physics, and engineering. For example, groups are used to study symmetry in geometry, to encode information in cryptography, and to model the behavior of physical systems.

Rings

A ring is a set of elements R with two operations, addition (+) and multiplication (*), that satisfy the following axioms:* Associativity of addition: For all a, b, and c in R, (a + b) + c = a + (b + c).

Commutativity of addition

For all a and b in R, a + b = b + a.

Identity for addition

There exists an element 0 in R such that for all a in R, 0 + a = a and a + 0 = a.

Inverse for addition

For each a in R, there exists an elementa in R such that a + (-a) = 0 and (-a) + a = 0.

• Associativity of multiplication

  For all a, b, and c in R, (a

• b)
• c = a
• (b
• c).

Distributivity of multiplication over addition

For all a, b, and c in R, a

• (b + c) = (a
• b) + (a
• c) and (a + b)
• c = (a
• c) + (b
• c).

Rings are used in a wide variety of applications, including number theory, algebra, and geometry. For example, rings are used to study the structure of numbers, to solve polynomial equations, and to model the geometry of curves and surfaces.

Fields

A field is a set of elements F with two operations, addition (+) and multiplication (*), that satisfy the following axioms:* All the axioms of a ring.

Multiplicative identity

There exists an element 1 in F such that for all a in F, 1

• a = a and a
• 1 = a.

Multiplicative inverse

For each nonzero element a in F, there exists an element a^(-1) in F such that a

• a^(-1) = 1 and a^(-1)
• a = 1.

Fields are used in a wide variety of applications, including number theory, algebra, and geometry. For example, fields are used to study the properties of polynomials, to solve algebraic equations, and to model the geometry of curves and surfaces.

Functions and Relations

In mathematics, a function is a relation between two sets, called the domain and the range, such that each element of the domain is associated with exactly one element of the range. A relation is a set of ordered pairs, where each pair consists of an element from the domain and an element from the range.

Functions can be represented in a variety of ways, including graphs, equations, and tables. The graph of a function is a plot of the ordered pairs in the function. The equation of a function is a mathematical expression that describes the relationship between the domain and the range.

The table of a function is a list of the ordered pairs in the function.

Types of Functions

There are many different types of functions, including linear functions, quadratic functions, and exponential functions. Linear functions are functions whose graphs are straight lines. Quadratic functions are functions whose graphs are parabolas. Exponential functions are functions whose graphs are curves that increase or decrease rapidly.

Applications of Functions

Functions have a wide range of applications in various fields, including mathematics, science, and engineering. In mathematics, functions are used to model relationships between variables. In science, functions are used to model physical phenomena. In engineering, functions are used to design and analyze systems.

Calculus: Math 1012 Foundations Of Mathematics

Calculus is a branch of mathematics that deals with change. It is used to study the rate of change of a function, the area under a curve, and the volume of a solid. Calculus has applications in many fields, including physics, engineering, economics, and biology.

Limits

A limit is a value that a function approaches as the input approaches a certain value. Limits are used to define derivatives and integrals, and they are also used to solve many other problems in calculus.

Derivatives

A derivative is the rate of change of a function. Derivatives are used to find the slope of a curve, the velocity of an object, and the acceleration of an object.

Integrals

An integral is the area under a curve. Integrals are used to find the volume of a solid, the work done by a force, and the probability of an event.

Geometry

Geometry is a branch of mathematics that deals with the properties and relationships of points, lines, planes, and angles. It is a fundamental subject in mathematics and has applications in many fields, including architecture, art, and engineering.

Some of the basic concepts of geometry include:

• Pointsare the most basic elements of geometry. They have no size or shape and are represented by a single dot.
• Linesare one-dimensional objects that extend infinitely in both directions. They are represented by a straight line segment.
• Planesare two-dimensional objects that extend infinitely in all directions. They are represented by a flat surface.
• Anglesare formed by two rays that share a common endpoint. They are measured in degrees.

Geometric Shapes

There are many different types of geometric shapes, each with its own unique properties. Some of the most common shapes include:

• Trianglesare three-sided polygons. They can be classified as equilateral (all sides are equal), isosceles (two sides are equal), or scalene (no sides are equal).
• Quadrilateralsare four-sided polygons. They can be classified as squares (all sides are equal and all angles are right angles), rectangles (all sides are equal and opposite angles are equal), parallelograms (opposite sides are parallel), or trapezoids (one pair of opposite sides is parallel).

• Circlesare two-dimensional shapes that are defined by a center point and a radius. The radius is the distance from the center point to any point on the circle.

Applications of Geometry

Geometry has many applications in the real world. Some of the most common applications include:

• Architecture: Geometry is used to design buildings and other structures. Architects use geometric principles to create buildings that are both aesthetically pleasing and structurally sound.
• Art: Geometry is used to create art. Artists use geometric shapes and patterns to create paintings, sculptures, and other works of art.
• Engineering: Geometry is used to design machines and other objects. Engineers use geometric principles to create objects that are both functional and efficient.

Mathematical Proof

In mathematics, a proof is a logical argument that establishes the truth of a statement. Proofs are essential in mathematics, as they allow mathematicians to demonstrate that their claims are valid and to build a body of knowledge that is both reliable and coherent.

There are many different types of proofs, but the most common are direct proofs, indirect proofs, and proofs by contradiction. A direct proof shows that a statement is true by constructing a logical argument that leads from the axioms of mathematics to the desired conclusion.

An indirect proof shows that a statement is true by assuming that it is false and then showing that this leads to a contradiction. A proof by contradiction shows that a statement is true by assuming that its negation is true and then showing that this leads to a contradiction.

Here is an example of a direct proof:

Theorem:The sum of two even numbers is even.

Proof:Let aand bbe two even numbers. Then a= 2 mand b= 2 nfor some integers mand n. Therefore, a+ b= 2 m+ 2 n= 2( m+ n). Since m+ nis an integer, a+ bis even.

Here is an example of an indirect proof:

Theorem:The square root of 2 is irrational.

Proof:Suppose that the square root of 2 is rational. Then it can be written as a fraction a/ b, where aand bare integers and b≠ 0. Squaring both sides of this equation, we get 2 = a²/ b². Multiplying both sides by b², we get 2 b² = a². Therefore, a² is even.

Since the square of an odd number is odd, amust be even. Therefore, a= 2 cfor some integer c. Substituting this into the equation 2 b² = a², we get 2 b² = (2 c)² = 4 c². Dividing both sides by 2, we get b² = 2 c². Therefore, b² is even.

Since the square of an odd number is odd, bmust be even. Therefore, both aand bare even. But this contradicts the fact that a/ bis a fraction in lowest terms. Therefore, our assumption that the square root of 2 is rational must be false.

Therefore, the square root of 2 is irrational.

Here is an example of a proof by contradiction:

Theorem:There are infinitely many prime numbers.

Proof:Suppose that there are only finitely many prime numbers. Let p₁, p₂, …, p_nbe all of the prime numbers. Consider the number N= p₁p₂… p_n+ 1. Since Nis not divisible by any of the prime numbers p₁, p₂, …, p_n, Nmust be prime.

But this contradicts the fact that Nis greater than any of the prime numbers p₁, p₂, …, p_n. Therefore, our assumption that there are only finitely many prime numbers must be false. Therefore, there are infinitely many prime numbers.

Essential Questionnaire

What are the prerequisites for Math 1012?

Typically, students are expected to have a strong foundation in high school algebra and trigonometry.

How is Math 1012 different from other math courses?

Math 1012 focuses on the foundational concepts of mathematics, providing a deeper understanding of the underlying principles that govern mathematical operations and structures.

What are the career prospects for students who excel in Math 1012?

A strong foundation in Math 1012 opens doors to various careers in fields such as engineering, computer science, finance, and research.